Subtraction Patterns Across Place Values

Patrones de sustracción entre valores de posición

😎 Earlier, you learned about addition patterns across place values. 

Anteriormente, aprendiste sobre los patrones de adición a través de los valores de posición.

They look like this:

Se ven así:

5 + 3 = 8
50 + 30 = 80
500 + 300 = 800
5,000 + 3,000 = 8,000

5 + 3 = 8. 50 + 30 = 80. 500 + 300 = 800. 5,000 + 3,000 = 8,000

Do you think subtraction follows a similar pattern too? 🤔

¿Crees que la resta también sigue un patrón similar?

Let's find out! 😃

Averigüémoslo.

Place Values Review

Revisión de los valores del lugar

1
10
100
1,000

1. 10. 100. 1,000

Can you tell what the place value of each '1' is?

¿Puedes decir cuál es el valor posicional de cada "1"?

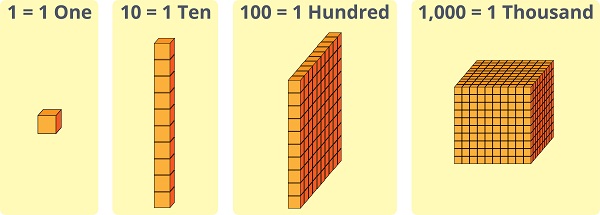
Very good!

¡Muy bien!

Subtraction Patterns Across Place Values

Patrones de sustracción entre valores de posición

Let's try subtracting two 1-digit numbers.

Intentemos restar dos números de 1 dígito.

6 - 2 = 4

6 menos 2 = 4

👉 Now, let's try subtracting the same digits, at increasing place values.

Ahora, intentemos restar los mismos dígitos, con valores de posición crecientes.

60 - 20 = 40

60 menos 20 = 40

600 - 200 = 400

600 menos 200 = 400

6,000 - 2,000 = 4,000

6.000 menos 2.000 = 4.000

Do you see a pattern? 🤔

¿Ves un patrón?

6 - 2 = 4
60 - 20 = 40
600 - 200 = 400
6,000 - 2,000 = 4,000

6 menos 2 = 4. 60 menos 20 = 40. 600 menos 200 = 400. 6.000 menos 2.000 = 4.000

Yes! 😎 These subtraction equations do follow a pattern!

¡Sí! ¡Estas ecuaciones de sustracción siguen un patrón!

👉 Let's try another example.

Probemos con otro ejemplo.

9 - 8 = 1
90 - 80 = 10
900 - 800 = 100
9,000 - 8,000 = 1,000

9 menos 8 = 1. 90 menos 80 = 10. 900 menos 800 = 100. 9.000 menos 8.000 = 1.000

These subtraction equations follow the pattern too! 🤗

¡Estas ecuaciones de sustracción también siguen el patrón!

So, what is the pattern? 🤔 

Entonces, ¿cuál es el patrón?

     When two digits are subtracted at increasing place values, their difference follows the same place value pattern as they do.

Cuando se restan dos dígitos con valores de posición crecientes, su diferencia sigue el mismo patrón de valor de posición que ellos.

Subtraction Patterns in Bigger Numbers

Patrones de sustracción en números más grandes

Now, let's see if subtraction patterns also hold true for bigger numbers.

Ahora, veamos si los patrones de sustracción también son válidos para números más grandes.

👉 Let's try subtracting 7 from 15, at different place values.

Intentemos restar 7 a 15, con diferentes valores de posición.

15 - 7 = 8
150 - 70 = 80
1,500 - 700 = 800
15,000 - 7,000 = 8,000

15 menos 7 = 8. 150 menos 70 = 80. 1.500 menos 700 = 800. 15.000 menos 7.000 = 8.000

Yes! 🤓 These numbers follow the pattern as well!

¡Sí! ¡Estos números también siguen el patrón!

👉 Let's try subtracting even bigger numbers.

Intentemos restar números aún más grandes.

67 - 41 = 26
670 - 410 = 260
6,700 - 4,100 = 2,600
67,000 - 41,000 = 26,000

67 menos 41 = 26. 670 menos 410 = 260. 6.700 menos 4.100 = 2.600. 67.000 menos 41.000 = 26.000

They follow the pattern too!

¡Ellos también siguen el patrón!

So, subtraction equations, just like addition, follow patterns across place values. ✅

Así, las ecuaciones de resta, al igual que las de suma, siguen patrones a través de los valores de posición.

Review

Revise

      When subtracting numbers that end with the same number of zeroes, subtract the non-zero digits, and then add the zeroes back to the difference!

Al restar números que terminan con el mismo número de ceros, resta los dígitos que no son ceros y luego suma los ceros a la diferencia.

Great job! Now, practice what you just learned. You'll understand more and remember for longer.

Gran trabajo! Ahora, practica lo que acabas de aprender. Entenderás más y lo recordarás durante más tiempo.