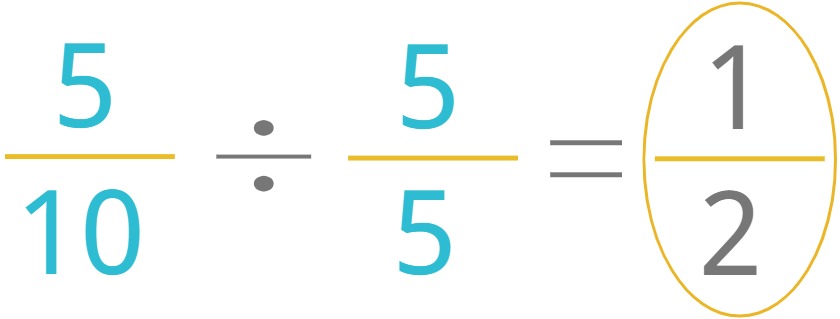How to Compare Decimals and Fractions

      Every fraction can be written as a decimal, and every decimal can be written as a fraction.

      Decimals and fractions are related because they both show parts of a whole.

For example, the decimal 0.5 is equal to the fraction 1/2.

0.5 is equal to "5 tenths". If we express that as a fraction, it would be 5/10.

If we simplify 5/10, we get 1/2.

      To simplify a fraction, we divide both numerator and denominator by the greatest factor that is common to both.

Using this knowledge, we can now compare decimals and fractions!

Comparing a Decimal with a Fraction

Which of these is larger?

0.6 ____ 2/4

We can't compare them right away because they're not in the same form. ❎ 

On the left side is a decimal and on the right side is a fraction.

So we have to convert, or turn, the fraction into a decimal first.

In this case, the fraction we want to convert is 2/4.

So we divide the numerator, 2, by the denominator, 4.

Then we solve the division problem.

2/4 in decimal form is 0.5. 🎉

Now, we can compare the two decimals.

0.6 _____ 0.5

0.6 > 0.5

We now know that 2/4 is equal to 0.5.

So we can replace 0.5 in the inequality with 2/4:

0.6 > 2/4 ✅

Great work. 👏

Another Example

Compare 0.65 and 3/4

First, convert 3/4 to a decimal.

We divide 3 by 4.

Then we solve to find the answer.

We see that...

3/4 in decimal form is 0.75

Now we can compare that with our other decimal.

0.65 _____ 0.75

Which symbol will make this statement true?

Let's compare the tenths place values.

We know that 6 is less than 7.

That means...

0.65 < 0.75

This means that...

0.65 < 3/4 ✅

Great job.

Last Example

Compare 3.65 to 3 and 3/5

The first step is to convert the mixed number 3 and 3/5 into a decimal.

When converting mixed numbers, we set aside the whole number first. Then we convert the fraction.

In this case, we set aside the whole number 3 and convert 3/5.

To convert the fraction, we start by dividing 3 by 5.

We solve to get the answer.

3/5 converted to a decimal is 0.6.

Let's add the decimal back to our whole number:

3 + 0.6 = 3.6

Now, we know that 3 and 3/5 is 3.6 in decimal form.

Let's go back to our original comparison statement.

Compare 3.65 and 3 and 3/5

Using the converted fraction, we can now re-write it like this.

3.65 _____ 3.6

We can add a 0 after the last digit of 3.6 to make it easier to compare the numbers. This does not change the value of the number.

3.65 _____ 3.60

Compare the tenths place first.

We see that they're the same, so we go to the hundredths place.

The first one has 5 hundredths, and the other one has 0 hundredths.

5 hundredths is greater than 0 hundredths.

This means that ...

3.65 > 3.60

Now we now know that...

3.65 > 33/5 ✅

Excellent work. 👏

Now, complete the practice.